\[\newcommand{\andop}{\mathrel{\&\!\&}} \newcommand{\orop}{\mathrel{\|}} \newcommand{\ff}{\mathsf{false}} \newcommand{\tt}{\mathsf{true}} \newcommand{\tm}[1]{\mathsf{#1}}\]

Predictive Parsing

Once you have an LL(1) parsing table, it is straightforward to implement a kind of parser called a predictive parser. It is predictive in the sense that it can predict what rule to use at every step - due to the grammar being LL(1).

In the Brischeme interpreter, the parser is responsible for converting a list of tokens into an abstract syntax tree, according to the grammar of the language.

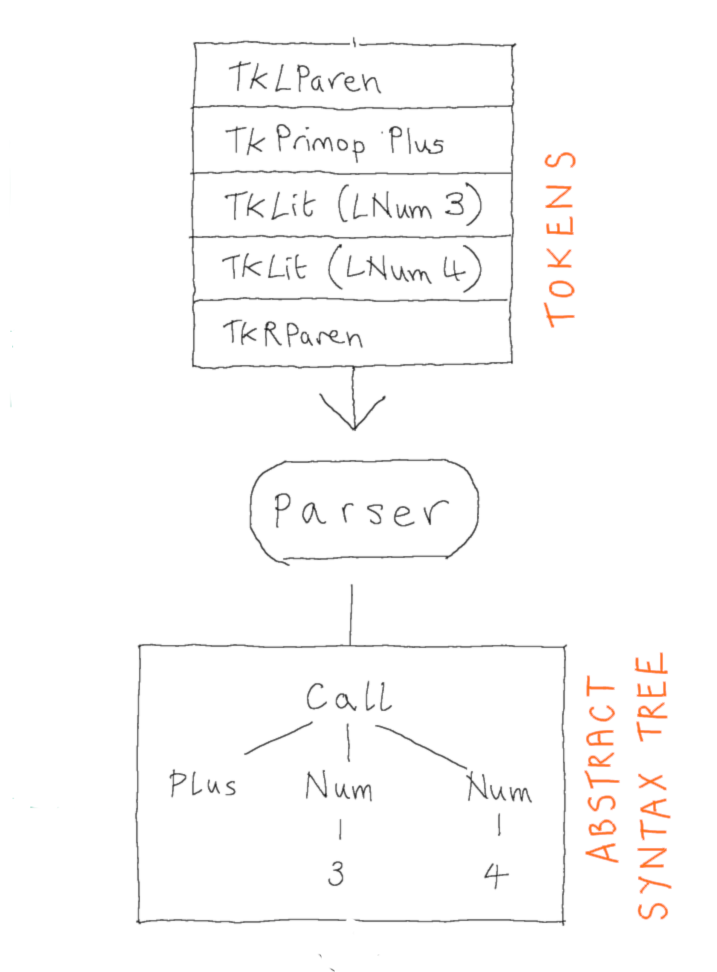
Recall that a token combines a classification of a lexeme (a kind of minimal meaningful substring of the input) along with, optionally, the lexeme itself. The tokens for Brischeme were defined as follows:

(** [token] is an enumeration of all possible tokens produced by the lexer *)
type token =
  | TkLit of literal
  | TkIdent of string
  | TkLParen
  | TkRParen
  | TkDefine
  | TkLambda
  | TkPrimOp of primop
  | TkEnd

The parser takes a string of tokens as input (i.e. a sequence of tokens) from which it must deduce the structure of the input string according to some grammar. So the grammar we will use is actually a grammar for deriving strings of tokens, rather than strings of characters. In other words, the tokens are the terminal symbols of grammar for the language (or, more properly their classifications are, since the structure of the language will not depend on, e.g. which particular integer we are looking at).

LL(1) Grammar for Brischeme

When the structure of a programming language is split into a description of the lexical elements and a separate grammar describing valid combinations of the lexical elements, the latter is known as the phrase structure of the language, and grammar we use for Brischeme is the following:

\[\begin{array}{rcl} \nt{Prog} &\Coloneqq& \nt{Form}\ \nt{Prog} \mid \tm{eof} \\[4mm] \nt{Form} &\Coloneqq& \nt{Atom}\\ \nt{Form} &\mid& \tm{(}\ \nt{CForm}\ \tm{)}\\[4mm] \nt{CForm} &\Coloneqq& \nt{Expr}\\ \nt{CForm} &\mid& \tm{define}\ \tm{ident}\ \nt{SExpr}\\[4mm] \nt{Atom} &\Coloneqq& \tm{literal} \mid \tm{ident}\\[4mm] \nt{IdentList} &\Coloneqq& \tm{ident}\ \nt{IdentList} \mid \epsilon\\[4mm] \nt{SExpr} &\Coloneqq& \nt{Atom}\\ \nt{SExpr} &\mid& \tm{(}\ \nt{Expr}\ \tm{)}\\[4mm] \nt{SExprList} &\Coloneqq& \nt{SExpr}\ \nt{SExprList} \mid \epsilon\\[4mm] \nt{Expr} &\Coloneqq& \tm{lambda}\ \tm{(}\ \tm{IdentList}\ \tm{)}\ \nt{SExpr}\\ \nt{Expr} &\mid& \tm{primop}\ \nt{SExprList}\\ \nt{Expr} &\mid& \nt{SExpr}\ \nt{SExprList}\\ \end{array}\]

For readability, we don’t use the OCaml names of the tokens, but there is a one-to-one correspondence between them and the terminal symbols of the grammar, which are:

\[\tm{literal} \quad \tm{ident} \quad ( \quad ) \quad \tm{define} \quad \tm{lambda} \quad \tm{primop} \quad \tm{eof}\]

We can construct a parse table for this grammar. It is a bit large, so I suggest using a tool like the following from Princeton: https://www.cs.princeton.edu/courses/archive/spring20/cos320/LL1/

	eof	(	)	define	ident	literal	lambda	primop
Prog	Prog ::= eof	Prog ::= Form Prog			Prog ::= Form Prog	Prog ::= Form Prog
Form		Form ::= ( CForm )			Form ::= Atom	Form ::= Atom
CForm				CForm ::= define ident SExpr			CForm ::= Expr	CForm ::= Expr
Atom					Atom ::= ident	Atom ::= literal
IdentList			IdentList ::= ε		IdentList ::= ident IdentList
SExpr		SExpr ::= ( Expr )			SExpr ::= Atom	SExpr ::= Atom
SExprList		SExprList ::= SExpr SExprList	SExprList ::= ε		SExprList ::= SExpr SExprList	SExprList ::= SExpr SExprList
Expr							Expr ::= lambda ( IdentList ) SExpr	Expr ::= primop SExprList

This tool creates the parse table for you, but it also adds a new non-terminal $S$ and a new terminal symbol \$, which is used to represent the end of input. However, we already have an explicit terminal symbol doing the same job ($\tm{eof}$, corresponding to token TkEnd), so these can be ignored (and I have removed them in the table above).

The parse table contains at most one rule per cell, so we are sure that this grammar is LL(1) and therefore can be used to create a predictive parser.

A Predictive Parser from an LL(1) Grammar

We start with some basic plumbing. Let’s suppose our input is going to be store in some mutable list of tokens:

tokens : (token list) ref

Much like in our lexer, we will use a small API to interface with the internal state. We need a way to initialise the state with a list of tokens (that we have been given by the lexer), a way to peek at the next element of the input (in this case, the next token), a way to consume it (actually remove it from the head of the list), and a way to raise errors. So we will assume we have four functions:

init : token list -> unit
peek : unit -> token
drop : unit -> unit
raise_parse_error : string -> unit

It’s useful to not only have a function that conditionally drops the next token if it is exactly the one specified (or otherwise raise an error) and, for those tokens that carry some data, like TkLit (LNum 3) to return the data LNum 3.

eat : token -> unit
eat_lit : unit -> sexp
eat_ident : unit -> string
eat_primop : unit -> primop

Then, to implement the parser, we simply make one new function for each non-terminal in the grammar. Each of these parsing functions takes no input (because it will access the next token from the mutable reference instead) and returns some part of the abstract syntax tree. Each of these parsing functions will be responsible for parsing those strings that are derivable from the corresponding nonterminal int he grammar. So, for example, sExpr will parse s-expressions, identList will parse lists of identifiers, and so on.

let rec prog () : prog = 
  match peek () with
  | TkEnd -> []
  | TkLParen | TkLit _ | TkIdent _ -> 
      let frm = form () in
      let prg = prog () in 
      frm :: prg
  | _ -> raise_parse_error "program"

and form () : form =
  match peek () with
  | TkLParen -> 
      eat TkLParen; 
      let f = cform () in 
      eat TkRParen; 
      f
  | TkIdent _ | TkLit _ -> Expr (atom ())
  | _ -> raise_parse_error "form"

and cform () : form =
  match peek () with
  | TkDefine -> 
      eat TkDefine;
      let s = eat_ident () in
      let e = sexpr () in
      Define (s, e)
  | TkLParen | TkIdent _ | TkLambda | TkPrimOp _ -> Expr (expr ())
  | _ -> raise_parse_error "expression or definition"

and atom () : sexp =
  match peek () with
  | TkLit _ -> eat_lit ()
  | TkIdent _ -> 
      let s = eat_ident () in
      Ident s
  | _ -> raise_parse_error "atom"

and ident_list () : string list =
  match peek () with
  | TkIdent _ -> 
      let s = eat_ident () in
      let ts = ident_list () in
      s :: ts
  | TkRParen -> []
  | _ -> raise_parse_error "ident list"

and sexpr () : sexp =
  match peek () with
  | TkLParen -> 
      eat TkLParen;
      let e = expr () in
      eat TkRParen; e
  | TkIdent _ | TkLit _ -> atom ()
  | _ -> raise_parse_error "s-expression"

and sexpr_list () : sexp list =
  match peek () with
  | TkLParen | TkIdent _ | TkLit _ -> 
      let e = sexpr () in
      let es = sexpr_list () in
      e :: es
  | TkRParen -> []
  | _ -> raise_parse_error "s-expression list"

and expr () : sexp =
  match peek () with
  | TkLParen | TkIdent _ | TkLit _ -> 
      let s = sexpr () in
      let ss = sexpr_list () in
      App (s, ss)
  | TkLambda ->
      eat TkLambda;
      eat TkLParen;
      let ss = ident_list () in
      eat TkRParen;
      let e = sexpr () in
      Lambda (ss, e)
  | TkPrimOp _ ->
      let p = eat_primop () in
      let es = sexpr_list () in
      Call (p, es)
  | _ -> raise_parse_error "expression"

The implementation strategy is straightforward, for each non-terminal $X$ we perform a case analysis on the next token $a$ of the input, and then we “execute” the unique parsing rule that is listed in the parsing table with row $X$ and column $a$. Otherwise, if that cell of the table is empty, we raise an exception.

What is meant by “execute” a parsing rule. The idea is to view the RHS of a rule $X \Coloneqq \beta$ as a strategy for parsing $X$ things. The RHS $\beta$ is a sentential form, a sequence of terminals and non-terminals, and the idea is that:

a terminal $a$ is read as an instruction to consume exactly that token from the input
a nonterminal $Y$ is read as an instruction to call the parsing function for $Y$ After “executing” the sentential form, we return the corresponding piece of the abstract syntax tree.

For example, consider the nonterminal $\nt{IdentList}$ which is used to derive sequences of identifiers (used when describing the formal parameters of a lambda function), such as: foo x y. Identifers are represented in the abstract syntax tree simply as strings, and lists of identifiers are represented simply as lists of strings (see e.g. the argument of AST constructor Lambda), so we will have a parsing function ident_list : unit -> string list.

To see how this function should behave, we consult the $\nt{IdentList}$ row of the parsing table. This row has only two non-empty cells, those for the terminals ) and ident:

\[\begin{array}{|c|c|c|}\hline \text{Nonterminal} & \tm{(} & \tm{ident} \\\hline \nt{IdentList} & \nt{IdentList} \Coloneqq \epsilon & \nt{IdentList} \Coloneqq \tm{ident}\ \nt{IdentList} \\\hline \end{array}\]

We start the function by analysing the next token of the input to see if it corresponds to one of these two terminals, i.e. token TkRParen or a token of shape TkIdent s. If it is TkRParen then we should proceed by “executing” the rule $\nt{IdentList} \Coloneqq \epsilon$. If it is of shape TkIdent s then we should proceed by “executing” the rune $\nt{IdentList} \Coloneqq \tm{ident}\ \nt{IdentList}$. In any other case, the corresponding cell of the row is empty, which means we have no hope of deriving this token, and so we raise a parse error.

  let ident_list () : string list =
    match peek () with
    | TkRParen -> (* proceed according to IdentList ::= ε *)
    | TkIdent _ -> (* proceed according to IdentList ::= ident IdentList *)
    | _ -> raise_parse_error "ident list"

The RHS of the former is the empty sentential form, so there are no instructions to perform. The rule derives the empty string, which corresponds to the empty list of identifiers []. The RHS of the latter tells us to first consume the TkIdent _ token and then recursively call identList. This corresponds to the list of identifiers that is made by putting the consumed ident on the front of the list returned by recursively calling identList, so we use eat_ident to consume this first ident token and return the string data (the name of the identifier) and then cons this onto the list returned from the recursive call.

let ident_list () : string list =
  match peek () with
  | TkRParen -> (* execute: ε *)
      []
  | TkIdent _ -> (* execute: ident IdentList *)
      let s = eat_ident () in    (* ident *)
      let ts = ident_list () in  (* IdentList *)
      s :: ts
  | _ -> raise_parse_error "ident list"

Exactly the same pattern is used to implement all of the other parsing functions.

Then, to use the parsing functions, we simply need to take the input string, lex it to obtain a list of tokens and then “call” the start symbol prog ():

(** [parse_prog s] returns the AST for the program written in string [s] *)
let parse_prog (s:string) : prog =
  tokens := lex s;
  prog ()